摘要：
如何从中发现隐藏的关联关系成为一项重要任务，随着数据的大规模积累。同时保留尽可能多的原始信息，能够将高维数据转化为更低维度的特征空间，而主成分分析（PrincipalCompone... 如何从中发现隐藏的关联关系成为一项重要任务，随着数据的大规模积累。同时保留尽可能多的原始信息，能够将高维数据转化为更低维度的特征空间，而主成分分析（PrincipalComponentAnalysis,PCA）作为一种常用的降维技术。详细解析主成分分析的原理和步骤、本文将以一个具体的主成分分析例题为例、并探讨其在数据分析中的应用。
1.原始数据的特征和问题陈述：并明确问题的核心、解读数据的背景和目标。
2.主成分分析原理简介：阐述其基于协方差矩阵的思想，介绍主成分分析的基本原理和数学推导。
3.数据预处理：如缺失值处理、讲解数据预处理的重要性和方法，标准化等。
4.协方差矩阵计算：并解释其在主成分分析中的作用、详细说明协方差矩阵的计算过程。
5.特征值和特征向量：以及它们在主成分分析中的重要性，解释特征值和特征向量的概念。
6.特征值与解释方差：阐述如何选择保留的主成分数量，讨论特征值与解释方差之间的关系。
7.主成分的计算：包括对特征向量的选择和排序、描述如何计算主成分。
8.主成分解释力度：即主成分与原始变量之间的关系程度、探讨主成分的解释力度。
9.主成分贡献率和累计贡献率：解释主成分贡献率和累计贡献率的概念及其在主成分分析中的意义。
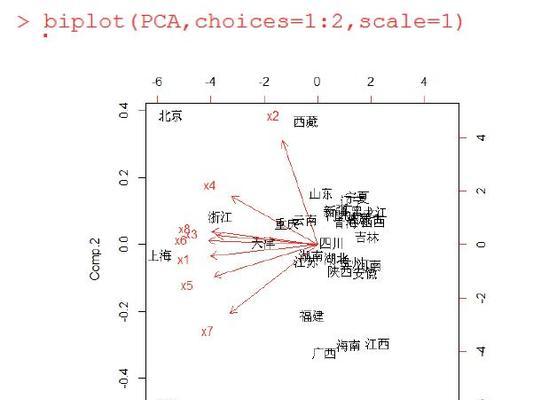
10.主成分图解析：探讨主成分之间的关系，展示主成分图并解读图中的信息。
11.主成分重构和回归系数：说明其在预测中的应用，介绍主成分的重构过程和回归系数的计算方法。
12.主成分分析在降维中的应用：并说明其在实际问题中的应用场景、探讨主成分分析在降维处理中的优势和适用性。
13.主成分分析的局限性和注意事项：避免在应用过程中的误区、列举主成分分析的局限性和注意事项。
14.主成分分析与其他降维技术的比较：如线性判别分析和因子分析等，对比主成分分析与其他常用的降维技术。
15.主成分分析的未来发展趋势：并提出进一步研究的方向，展望主成分分析在未来的发展趋势。
掌握了主成分分析的基本步骤、我们深入理解了主成分分析的原理和应用、通过本文的解析与讨论，并了解了其在数据分析中的重要性和局限性。为后续的建模和预测提供有力支持、我们可以更好地理解数据背后的本质关系，通过主成分分析，提取重要特征并降低数据维度。
